######图的表示呢分为邻接矩阵和邻接链表。其主要算法层出不穷,这里主要介绍最短路径的ford和dijsktra,单源最短路径,思维可能有点局限,有什么好的想法可以联系我,代码有如雷同,不怨俺.
(数组d[]表示求解的各点最短路径,from表示来源点,to表示目的点,cost表示权值,e(i,j)表示从i到j的边 )
题目来源: 小木乃伊到我家
输入描述:
第一行输入两个整数n和m(2<=n<=m<=200000),分别表示有n座城市和m条路,城市编号为1~n(快递姐姐所在城市为1,AA所在城市为n)。
接下来m行,每行输入3个整数u,v,w(u,v<=n,w<=100000),分别表示城市u和城市v之间有一条长为w的路。
输出描述:
输出结果占一行,输出快递姐姐到达AA家最短需要走多远的路,如果没有路能走到AA家,则输出“qwb baka”(不用输出双引号)。
示例1
1
2
3
4
5
6
7
8
| 输入
4 4
1 2 1
2 3 2
3 4 3
2 3 1
输出
5
|
Ford 算法解决
递推公式呢就是 d[i]=min{d[j]+cost[i][j]}
但是这个效率比较低啊,时间O(e^2),这个算法程序就不详解了;
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
using namespace std;
#define MAX_E 200005
#define INF 0x3f3f3f3f
#include <time.h>
struct edge{int from,to,cost;};
edge es[MAX_E];
int d[MAX_E];
int V,E;
void WithMax()
{
for(int i=1;i<=V;i++)
d[i]=INF;
}
void the_short_path(int s)
{
WithMax();
d[s]=0;
while(1)
{
bool update=false;
for(int i=1;i<=E;i++){
edge e=es[i];
if(d[e.from]!=INF&&d[e.to]>(d[e.from]+e.cost))
{
d[e.to]=d[e.from]+e.cost;
update=1;
}
}
if(update==false) break;
}
}
int main()
{
while(cin>>V>>E)
{
clock_t start_time,end_time;
start_time=clock();
for(int i=1;i<=E;i++)
cin>>es[i].from>>es[i].to>>es[i].cost;
the_short_path(1);
if(d[V]==INF) cout<<"qwbbaka"<<endl;
else cout<<d[V]<<endl;
end_time=clock();
cout<<"运行时间: "<<(double)(end_time-start_time)/CLOCKS_PER_SEC<<endl;
}
return 0;
}
|
####迪杰斯特拉算法
-
引入(楼主可能是太特么懒了):
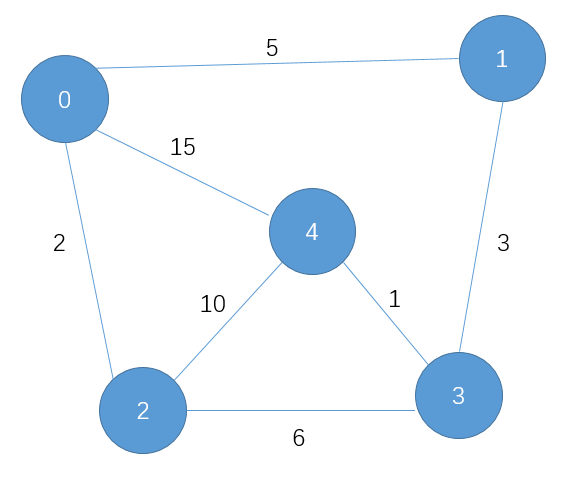
上图所示的图,求0到各个点的最短距离
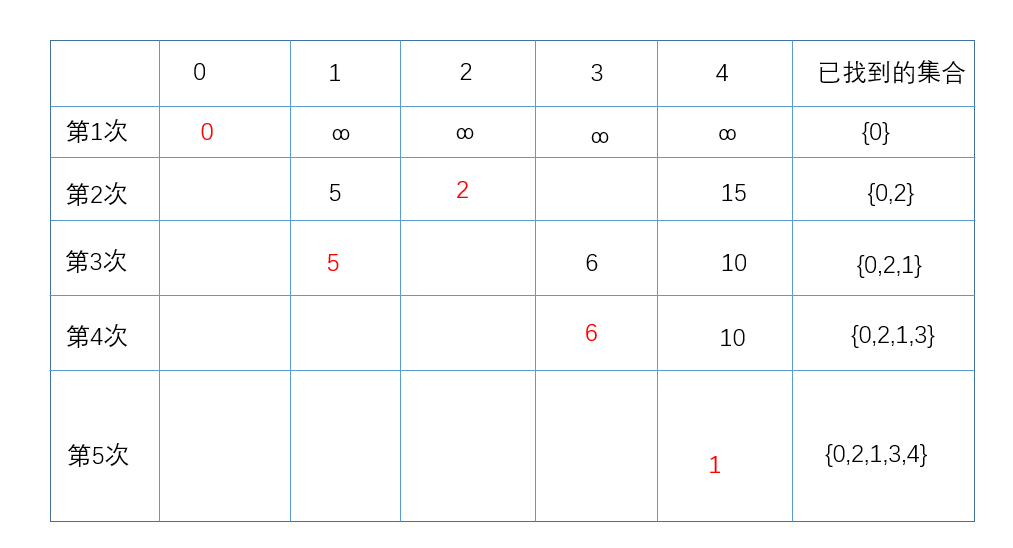
具体原理如下,最后填充的哪个点进集合的位置,就是加上之前的最小距离
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
| #include <iostream>
#include <cstdlib>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
#define MAX_A 200005
#define INF 0x3f3f3f
#define ll long long
#include <time.h>
struct node
{
ll to,cost;
node(){}
node(ll x,ll y)
{
to=x;
cost=y;
}
bool operator < (const node &a) const
{
return cost>a.cost;
}
};
ll V,E;
vector<node> G[MAX_A];
ll vis[MAX_A];
ll d[MAX_A];
void dijkstra()
{
fill(vis,vis+V+1,0);
fill(d,d+V+1,INF);
d[1]=0;
priority_queue<node> que;
que.push(node(1,0));
while(!que.empty())
{
node e=que.top();
que.pop();
if(vis[e.to]) continue;
vis[e.to]=1;
for(unsigned long i=0;i<G[e.to].size();i++)
{
ll to=G[e.to][i].to,cost=G[e.to][i].cost;
if(!vis[to] && d[to]>d[e.to]+cost)
{
d[to]=d[e.to]+cost;
que.push(node(to,d[to]));
}
}
}
}
int main()
{
ll f,t,c;
while(cin>>V>>E)
{
clock_t start_t,end_t;
start_t=clock();
for(ll i=1;i<=V;i++)
G[i].clear();
for(ll i=0;i<E;i++)
{
cin>>f>>t>>c;
G[f].push_back(node(t,c));
G[t].push_back(node(f,c));
}
dijkstra();
cout<<d[V]<<endl;
end_t=clock();
cout<<(double)(end_t-start_t)/CLOCKS_PER_SEC<<endl;
}
}
|



