先介绍下DFS
下面这张图呢是图的原来状态
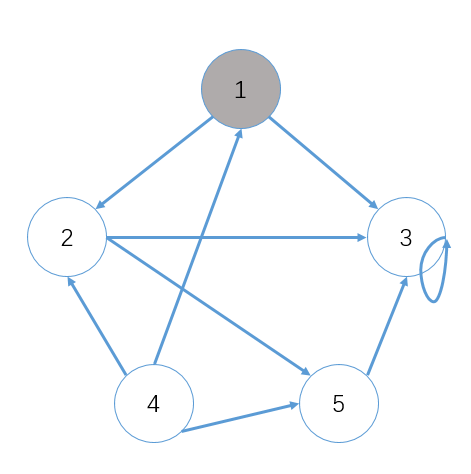
这个gif呢是其深度优先遍历的过程,ppt做的,可能会失真
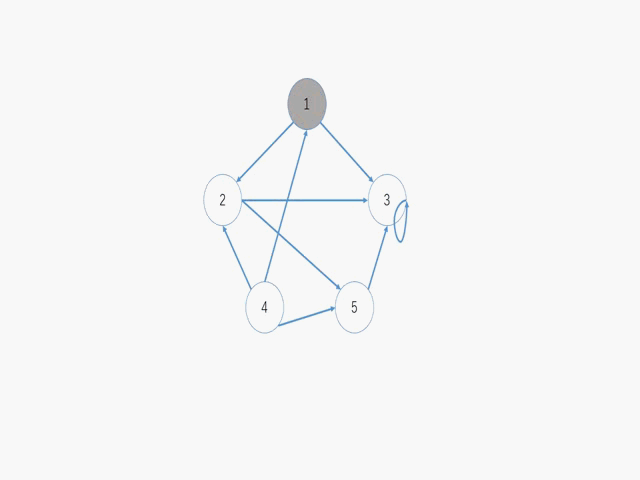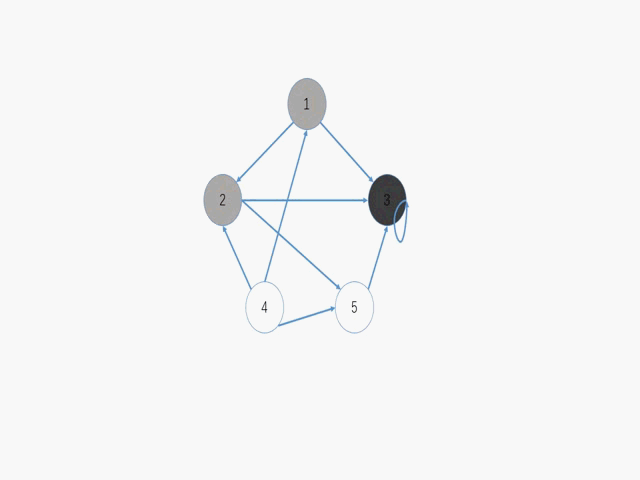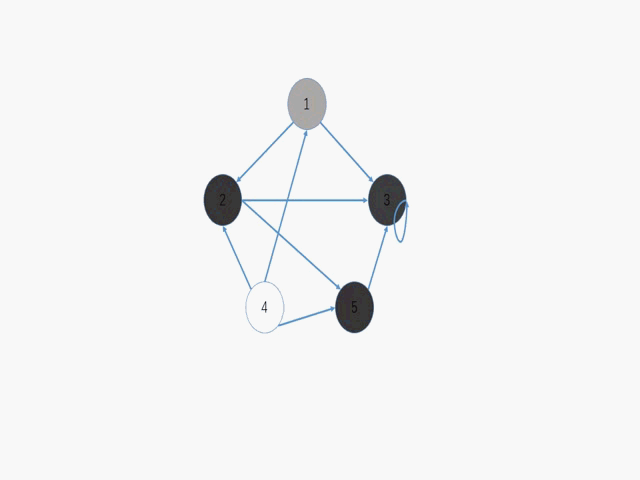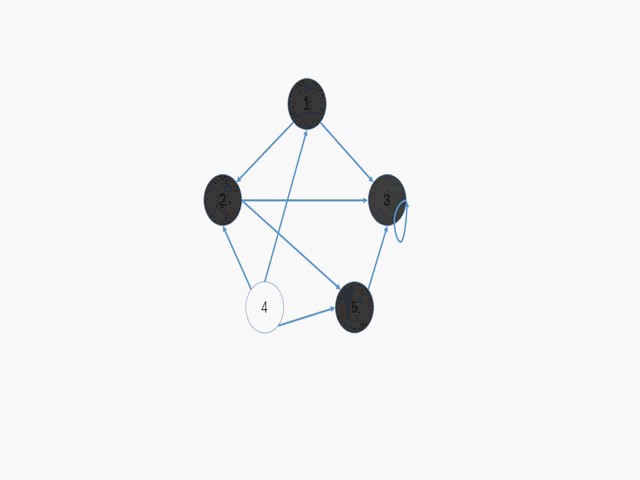
遍历的思想有了,但是对于非稀疏图来讲利用图的邻接矩阵遍历效果是不是更好。
那么代码就来了;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<iostream>
#include<queue>
#include<stack>
/*
图的深度优先搜索
数据结构中介绍需要用到栈的帮助
这里的栈用C++ STL的stack
*/
using namespace std;
#define number 5
//定义图的邻接矩阵
void DFS(int start);
int map[][5]=
{
0,1,1,0,0,
0,0,1,0,1,
0,0,1,0,0,
1,1,0,0,1,
0,0,1,0,0
};
//访问过的顶点
int visited[number + 1];
int main()
{
//初始化数组为0,表示一个也没访问
memset(visited, 0, sizeof(visited));
for (int i = 1; i <= number; i++)
{
if (visited[i] == 1)
continue;
DFS(i);
}
system("pause");
return 0;
}
void DFS(int start)
{
stack<int> stk;
//顶点入栈
stk.push(start);
//表示访问
visited[start] = 1;
bool IS_PUSH = false;//是否有新的顶点入栈
while (!stk.empty())
{
IS_PUSH = false;
int p = stk.top();
for (int i = 1; i <= number; i++)
{
if (map[p - 1][i - 1] == 1 && !visited[i])
//如果他俩联通,并且还没有访问过
{
visited[i] = 1;
stk.push(i);
IS_PUSH = true;//新顶点入栈
break;
}
}
if (!IS_PUSH)
{
cout << p << " ";
stk.pop();//顶点出栈
}
}
}
|
运行结果,看图就能看出来了,不过代码只是更简单点了
BFS
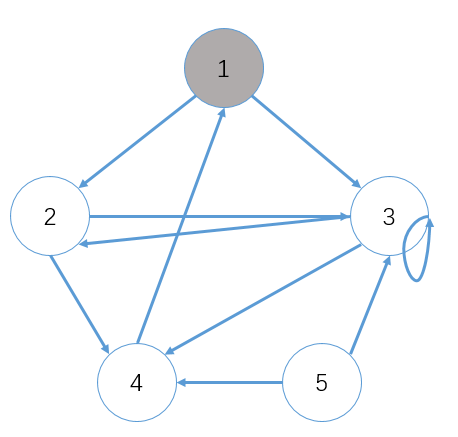
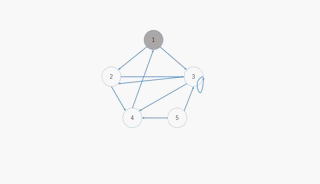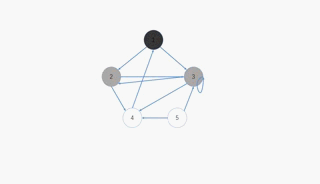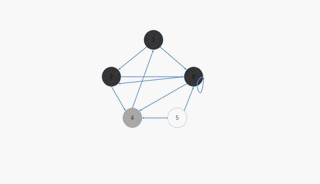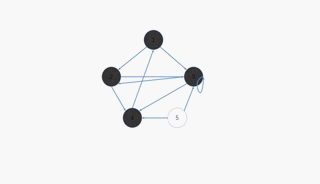
代码用到队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| void BFS(int start)
{
queue<int> que;
//顶点入队
que.push(start);
//表示访问
visited[start] = 1;
while (!que.empty())
{
int p = que.front();
cout << p << " ";
que.pop();
for (int i = 1; i <= number; i++)
{
if (map[p - 1][i - 1] == 1 && !visited[i])
//如果他俩联通,并且还没有访问过
{
visited[i] = 1;
que.push(i);
}
}
}
}
|







